

ch7에서 배운 Q-learning 알고리즘은 위와 같았습니다. 한 time step의 data를 수집한 뒤 target 값을 바탕으로 sudo-gradient를 통해 Q-function을 update하는 방식이었습니다. 이 알고리즘은 두 가지 문제를 가지고 있습니다.

매 time-step의 data는 correlated 되어있다. 이는 bias를 유발한다.
1번은 당연한 문제입니다. 로봇이 이동하는 상황이라면 $t+1$의 data는 $t$의 상황에서 크게 벗어나지 않을 것입니다. 하지만 우리의 학습 목표는 언제나 generalization이기 때문에, data 자체의 편향이 문제가 됩니다.
$y_i$가 실제로는 $ϕ$와 연관되어 있기 때문에, 올바른 gradient descent와 달리 moving target으로 인한 불안정성이 존재한다. → 이건 TD Error 자체에 내재된 문제
2번은 update 식이 pseudo-gradient이기 때문에 발생합니다. 올바른 objective function의 gradient를 구한게 아니라는 것이죠. 하지만 $\text{max}$ 함수가 들어있는 이상 실제 gradient를 구하는 것은 너무나 복잡합니다. 이 두 문제를 해결하는 방법에 대해 논의합니다.
Temporal Difference Learning
Bootstrapping
1번 문제를 해결하기 위해 떠올려볼 수 있는 방법은 batch를 이용하는 것입니다. batch를 이용하면 data의 편향성이 줄어들 것이기 때문입니다. 위와 같이 여러 개의 환경을 동시에 작동시켜 data를 얻을 수 있죠.
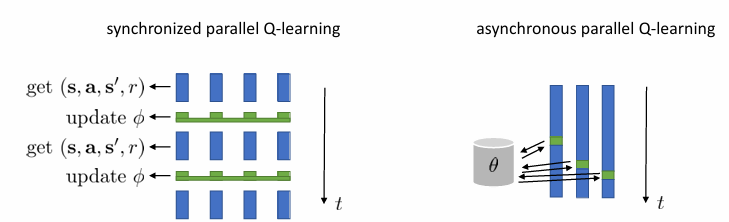
여기서는 새로운 방식을 제시합니다. 어차피 off-policy로 해도 되는데 online으로 작동시킬 필요가 있냐는 것입니다. 그냥 data를 엄청 많이 수집해놓고, 잘 섞어서 random sampling 하자는 것입니다. ⇒ 연속적인 데이터로 인한 bias 방지
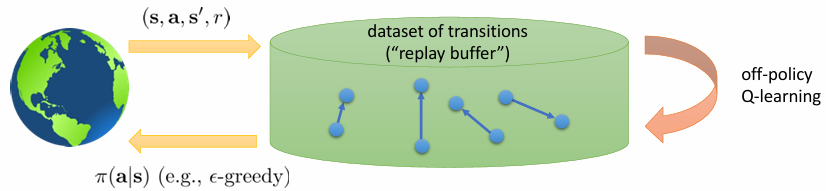
이렇게 random sampling할 수 있게 sample을 담아둔 것을 reaplay buffer $\mathcal{B}$라고 부릅니다. 그런데 어디 이상한 데서 policy를 데려오는 것도 무리기 때문에, $\epsilon$-greedy 방법을 이용해서 중간중간 data를 보충하고, random으로 섞어서 다시 뽑고..의 방식을 이용합니다. 이렇게 정리된 알고리즘은 다음과 같습니다.

fitted Q-iteration과 다른 점은 update 식입니다. $\phi$를 $\argmin$을 찾을 때까지 fitting 하는 fitted Q-iteration과는 다릅니다.
x