Reasoning about performance from first principles

When trying to optimize performance on a computer, we can simplify the hardware into two things [1]

1. some number of compute execution units with a fixed number of maximum possible floating point operations per seconds (FLOPS/s)
2. memory bus that can move a fixed number of bytes/s into the compute units.

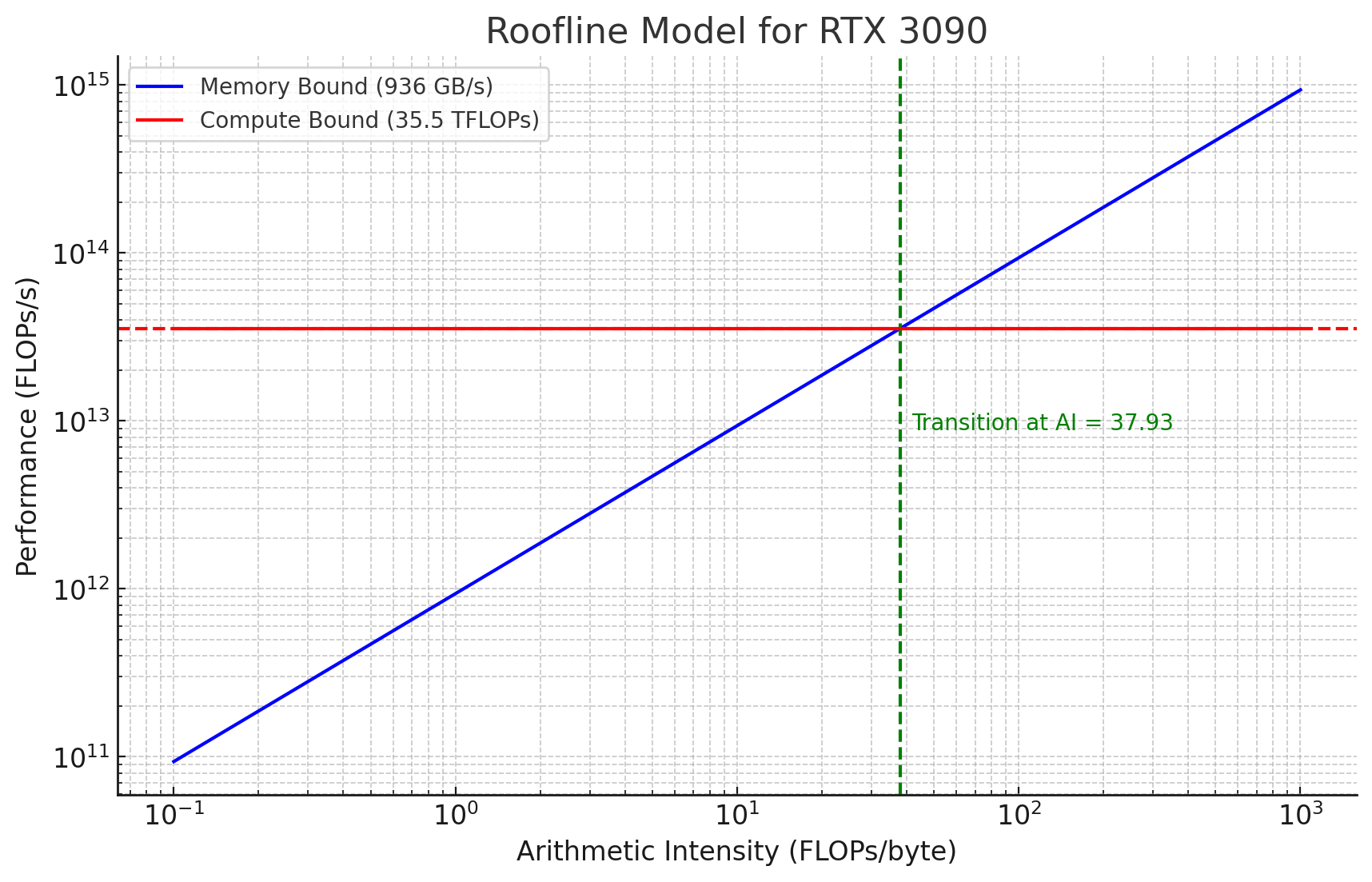
For the RTX 3090 this is around 35.5 TFLOPs with a max global memory bandwidth of 936 GB/s. We can idealize the program running on the computer as loading K bytes and performing N operations with each byte, giving us the arithmetic intensity. When trying to understand what the upper bound of tasks that can be performed per second, we can use the equation below.

By multiplying the memory bandwidth by the arithmetic intensity we adjust for the fact that each loaded byte results in K operations. The resulting number P is the minimum of the memory bandwidth (adjusted for arithmetic intensity) and the theoeretical FLOPS/s. This tells us the upper bound for performance as well as whether the program will be compute-bound or memory-bound. This beautiful abstraction is true for any machine based on the Von Neumann architecture, not just GPUs.

‍

‍

The plot above shows a blue line, which is AI * Mem-Bandwidth, as well as a FLOPS/s line which is horizontal. The point at which the blue line crosses the red-line shows what the arithmetic intensity of a program would need to be to fully saturate the 3090s compute units. We need to perform ~38 operations per loaded byte to get to this point! Lets look at arithmetic intensity for vector addition/matrix multiplication, and quantify their AI.

‍

FP32 Vector Addition (4 bytes per element)

1. Load bytes for Vector A.
2. Load bytes for Vector B.
3. Perform ~  FP32 add operations to add Vector A & B.
4. Store bytes.

Arithmetic Intensity (AI) is operations/bytes or 0.0833.

Vector addition is heavily memory bound, since the arithmetic intensity is so low.

‍

FP32 Matrix Multiplication (all matrix dimensions N for simplicity)